天池-工业蒸汽量排放预测1
链接:工业蒸汽量预测_学习赛_赛题与数据_天池大赛-阿里云天池的赛题与数据 (aliyun.com)

数据探索
变量识别
通过变量类型,数据类型等方面分析,常见的有:字符型变量,数值型变量,连续性变量,类别性变量
变量分析
单变量分析
连续性变量需要统计数据的中心分布趋势与变量分布
类别性变量使用频次或者占比表示每一个类别的分布情况。可用柱状图可视化分布情况
双变量分析
双变量分析主要是为了洞察各变量之间的关系
1. 连续型与连续型
- 绘制散点图观察是线性还是非线性
- 计算相关性
散点图如下所示:
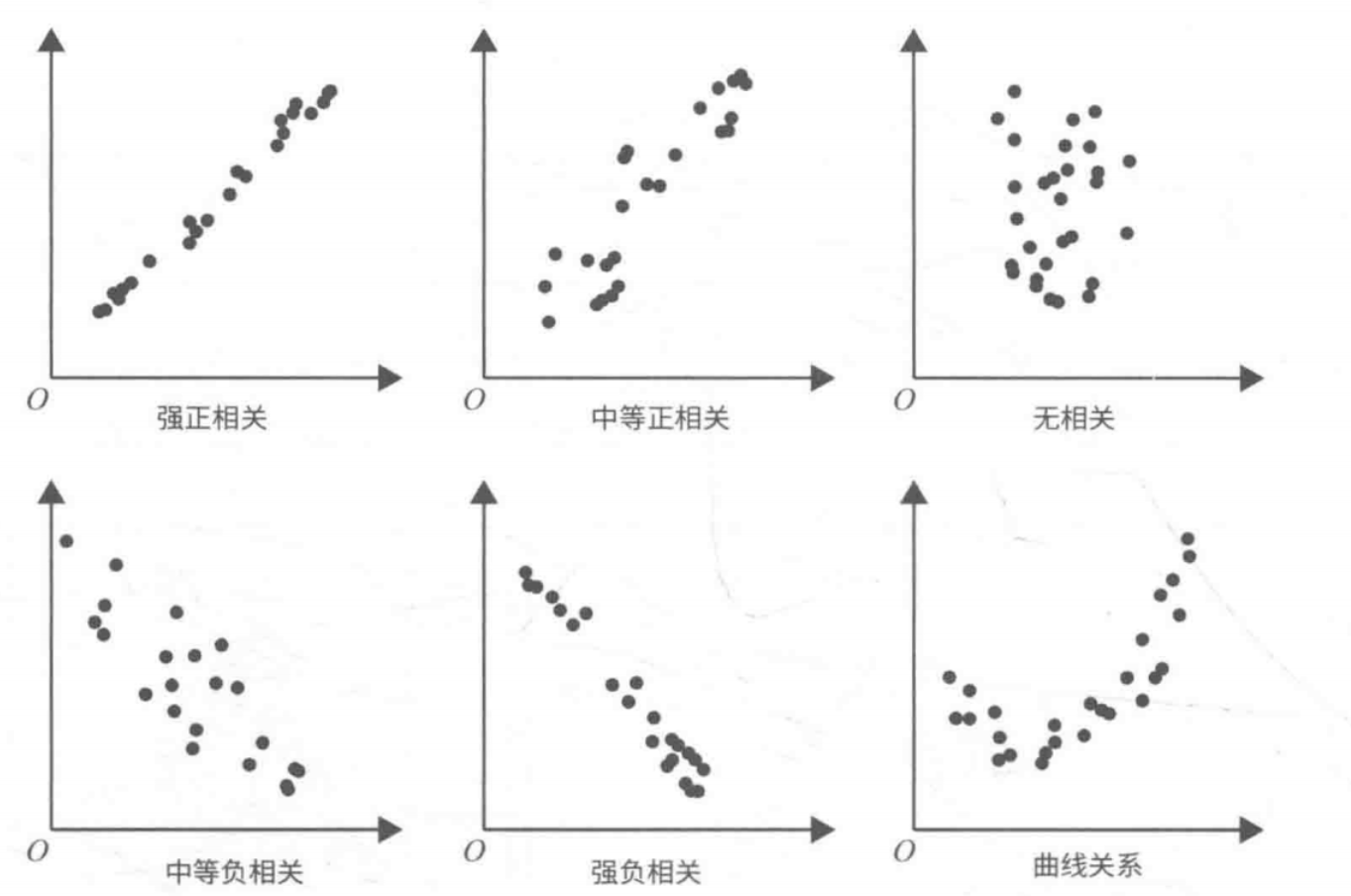
2. 类别性与类别性
- 双向表,建立频次(次数)与频率(占比)的表格
- 堆叠柱状图,更直观
- 卡方检验,用于两个和两个以上样本率及两个二值型离散变量的关联性分析,即比较理论频次与实际频次的吻合程度
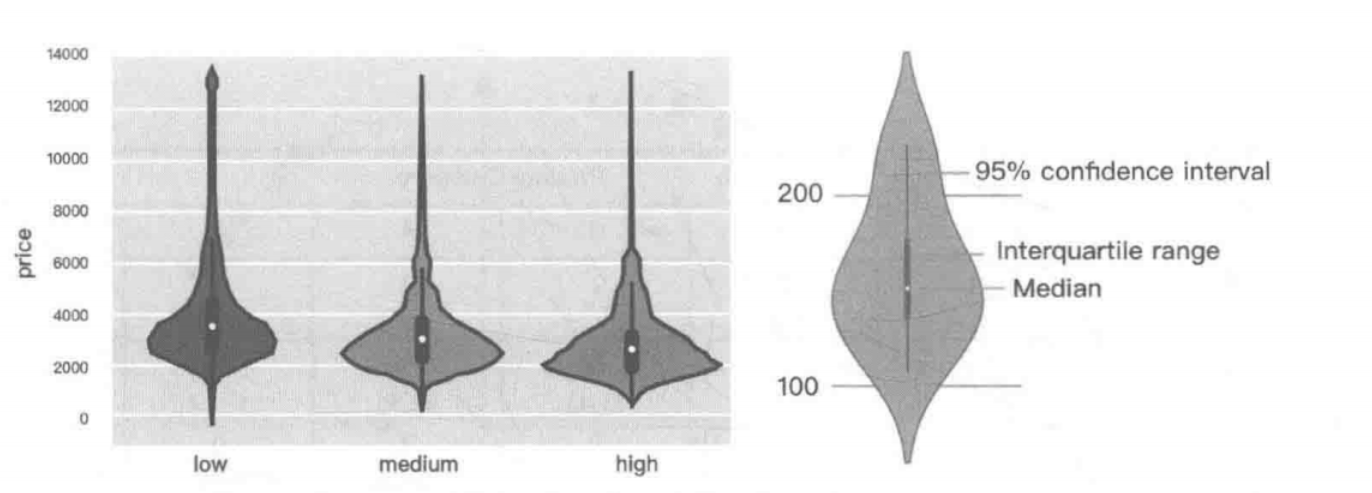
3. 类别性与连续性
- 小提琴图,可以在分析变量在不同类别时,另一个连续变量的分布情况,如下图
缺失值处理
产生原因就不说了,反正没啥实际用处,tmd都得处理,处理办法如下:
1. 删除:成列删除和成对(行)删除
2. 平均值,众数,中值填补:最常用的办法
3. 建立模型填充:好处:规范;坏处:模型有问题就G
异常值处理
异常值的影响为增加错误方差,降低模型的拟合能力
1. 如何检测?(异常值通常取决于业务理解)
- 箱线图
2. 处理办法
- 删除:很小或很少的直接删
- 转化:如取对数,减少极值影响
- 填充:平均值,中值等,前提是人为的,模型预测也可
- 区别对待:真的很多就正常的分一组,异常的分一组,然后模型合并
变量转换
对变量的分布不平均的时候,需要对变量的取值区间进行转换,使其落在合理的区间内。如下,当需要基于正态分布假设前提的模型的时候, 进行对数转换
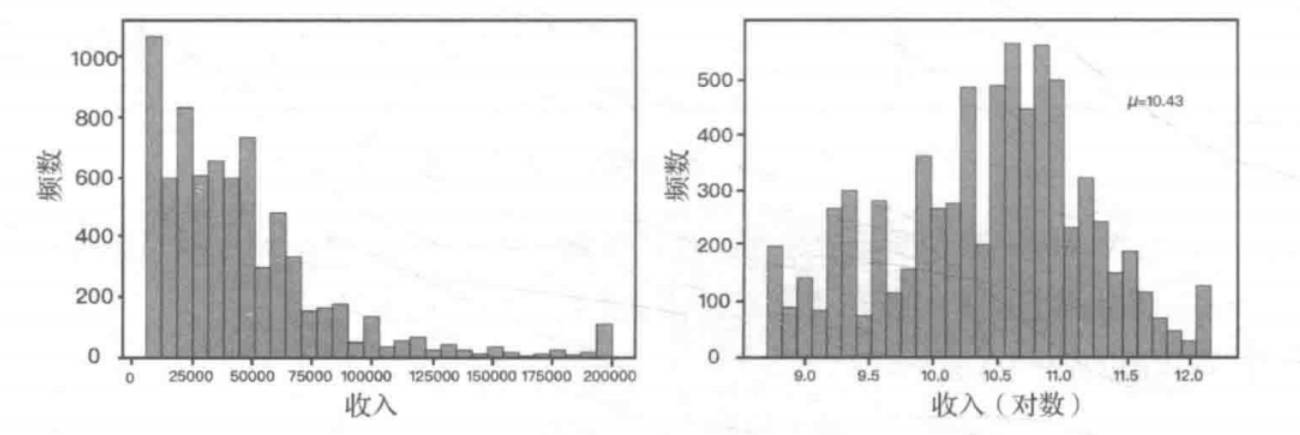
1. 方法

- 对数转换:右转左,左转右,负或非零不能转
- 取平方根或立方根:有波形影响
- 变量分组
新变量生成
目的是为了与目标变量有更好的相关性
1. 方法
- 创建派生变量:将Mr,Mrs,Miss作为新变量
- 哑变量
常用函数与作图
# 读取txt,\t为分隔
data = pd.read_csv('url', sep='\t', encoding='?')
# 查看基本信息
data.info()
# 查看统计信息
data.describe()# 箱线图
fig = plt.figure(figsize=(4, 6))
sns.boxplot(train_data['V0'], orient='v', width=0.5)筛选出异常值
# 直方图
plt.figure(figsize=(10, 5))
ax = plt.subplot(1, 2, 1)
sns.distplot(train_data['V0'], fit=stats.norm)# q-q图,查看是否符合正态发布
ax = plt.subplot(1, 2, 1)
res = stats.probplot(train_data['V0'], plot=plt)非正态分布的数据可以进行数据变换
# KDE,对直方图的加窗平滑
plt.figure(figsize=(8,4), dpi=150)
ax = sns.kdeplot(train_data['V0'], color='Red', shade=True)
ax = sns.kdeplot(test_data['V0'], color='Blue', shade=True)
ax.set_xlabel('V0')
ax.set_ylabel('Frequency')
ax = ax.legend(['train', 'test'])在test和train中如果分布不一致,模型的泛化能力会变差,需要删除
# 线性回归关系图,分析变量之间的线性回归关系
fcols = 2
frows = 1
plt.figure(figsize=(8, 4), dpi=150)
ax = plt.subplot(1, 2, 1)
sns.regplot(x='V0', y='target', data=train_data, ax=ax,
scatter_kws={'marker':'.', 'alpha':0.3},
line_kws={'color':'k'})
plt.xlabel('V0')
plt.ylabel('target')
ax = plt.subplot(1, 2, 2)
sns.distplot(train_data['V0'].dropna())
plt.xlabel('V0')
plt.show()对于那些相关性不怎么重要的,就可以直接删去了
Box-Cox
转换为正态分布形式。该变换方法可以使线性回归方程在满足线性,正态性,独立性及方差齐性的同时还,又不丢失信息。需要先做归一化在B-C变换