强化学习2 马尔可夫决策过程(Markov Decision Process, MDP)
1 马尔可夫性质(Markov property)
对于天气预报而言,今天是否下雨只取决于前一天的天气情况,无关于前2345...n天的情况。这就是MP(马尔可夫性质,下文简称MP)
换句话来说,一个随机过程在给定现在状态及所有过去状态情况下,其未来状态的条件概率分布仅依赖于当前状态。给出公式如下
$$
p(X{t+1}=x{t+1}\mid X{0:t}=x{0:t})
p(X{t+1}=x{t+1}\mid X_t=x_t)
$$
此处假设随机变量$X_0, X_1, ..., X_T$为一个随机过程。公式代表的含义指需要看每个p的后半部分(|xxx),意思就是前面的都不用看,看个t就行。
MP也可以描述为给定当前状态时,将来的状态与过去状态是条件独立的。如果某一个过程满足马尔可夫性质,那么未来的转移与过去的是独立的,它只取决于现在。马尔可夫性质是所有马尔可夫过程的基础。
2 马尔可夫链(Markov chain)
这就是符合MP的一个系统,此处需要引入五元组之一
$$
s
$$
s(state)是马尔可夫过程(Markov process)中的随机变量序列,满足马尔可夫性,并且下一时刻的状态$s_{t+1}$ only depend on $s_t$.
设状态的历史为$h_t={s_1, s_2, ..., st}$,则MP满足以下条件
$$
p(s{t+1} \mid s_t)
p(s_{t+1} \mid ht)
$$
其实和1.1的内容大差不多,但本节可以映入一个状态转移矩阵(state transition matrix)P来描述状态$p(s{t+1}=s' \mid s_t=s)$。五元组大部分都是需要用到矩阵运算的,所有这样显的很高级(开玩笑的,主要是很好算)
$$
p =
\begin{pmatrix}
p(s_1 \mid s_1) & p(s_2 \mid s_1 & \cdots & p(s_N \mid s_1)) \
p(s_1 \mid s_2) & p(s_2 \mid s_2) & \cdots & p(s_N \mid s_2) \
\vdots & \vdots & \ddots & \vdots \
p(s_1 \mid s_N) & p(s_2 \mid s_N) & \cdots & p(s_N \mid s_N)
\end{pmatrix}
$$
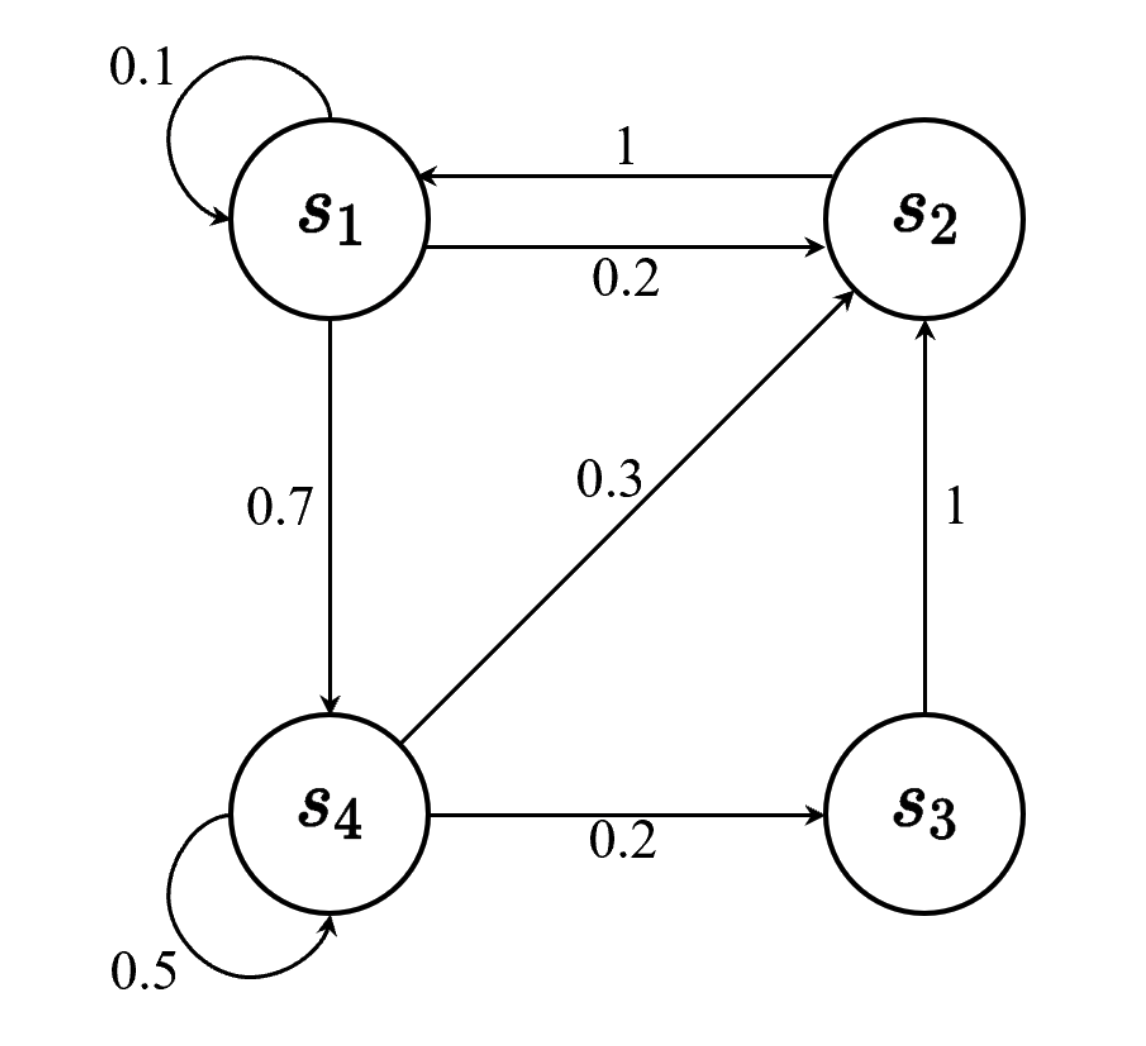
下图是一个离散情况的马尔可夫链实例,可以理解为走迷宫时,从state A 到state B的概率是多少
还有一个最经典的例子就是火星车,假设我们从$s_3$开始,可以获取如下三个轨迹(很多轨迹,我就举三个例子哈)
· $s_3, s_4, s_5, s_6, s_6$
· $s_3, s_2, s_3, s_2, s_1$
· $s_3, s_4, s_4, s_5, s_5$
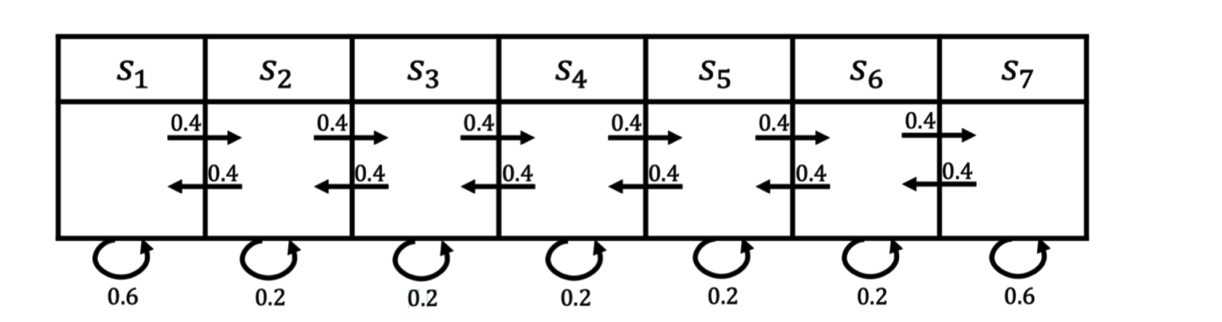
此处,我们获取了常见两元组
$$
<s, p>
$$
where $s$ is state and $p$ is the persentage of state transition
3 马尔可夫奖励过程(Markov reward process, MRP)
先引入元组,后文继续解释。在1.3阶段,变成了四元组
$$
<s, p, r, \gamma>
$$
MRP的本质就是MP+奖励函数(reward function),R是一个期望,表示当我们到达某一个状态的时候,可以获得多大的奖励(有奖励才知道这么走对不对是不),另行定义折扣因子$\gamma(0,1)$,这和回报有关(我们需要考虑长时期回报,短时期回报)
3.1 回报与价值函数
首先定义回报(return),可以理解为奖励加加加,如果机器人走一步只会获得当前state的奖励,那就是纯贪心算法,我们需要考虑未来会有什么样的回报,因此这是一个一元n次方程,即
$$
Gt = r{t+1}
+
\gamma r_{t+1}
-
\gamma^2 r_{t+2}
-
\gamma^3 r_{t+3}
-
...
-
\gamma^{T-t-1} r_{T}
$$
$T$为时间的一个序列。折扣越多。这说明我们更希望得到现有的奖励,对未来的奖励要打折扣。当我们有了回报之后,就可以定义状态的价值了,就是状态价值函数(state-value function)。对于马尔可夫奖励过程,状态价值函数被定义成回报的期望,即
$$
V^t(s) = \mathbb{E}[G_t \mid s_t=s]
$$
在得到 $g_t$后,我们就可以计算每个轨迹的r了,依旧以火星车为例,给定向量$R=[5, 0,0,0,0,0,0,10]$为奖励函数, $\gamma=0.5$的情况下计算
轨迹1: $0 + 0.5 \times0+0.25\times0+0.125\times10=1.25$
轨迹2: $0 + 0.5 \times0+0.25\times0+0.125\times5=0.625$
轨迹3: $0 + 0.5 \times0+0.25\times0+0.125\times0=0$
hints:
状态价值函数$V^t(s)$:处于状态 s,并且之后一直按照某种策略行动,我预期总共能得多少分。重点在于身处何地
价值函数:$V(s)$:分为状态价值函数和动作价值函数,前者为前者,后者为(状态+动作)有多好(Q函数,后文讲)
3.2 贝尔曼方程(Bellman equation)
这是$V^t(s)$的另一种表现形式,后文都用的是这个,别管我什么,推导过程一大堆我懒的看,但就是好!而且表达的也很简洁
$$
V^t(s) = R(s) + \gamma\sum{s'\in S}p(s' \mid s)V(s')
$$
其中,$R(s)$为即时奖励(也就是当前state的奖励),$\gamma\sum{s'\in S}p(s' \mid s)V(s')$为未来奖励的折扣综合。其实和式7是一样的,只不过换了一种方式
贝尔曼方程定义了当前状态与未来状态之间的关系。未来奖励的折扣总和加上即时奖励,就组成了贝尔曼方程
其实贝尔曼方程决定了状态之间的迭代关系,有了迭代这一步就可以算出他的解析解,从而知道$V^t(s)$的值(因为他包含目前到未来的总奖励)。但是问题就在于。
-
如果用矩阵形式计算的话,计算量很大(n的三次方)
-
核心在于$p(s' \mid s)$,但是在实际上我们是不知道的(举个例子,机器人走网格)。只有完全知道环境模型的情况下才有这个数(有模型情况,下一章介绍)
所以,才有后续的计算方法,比如说蒙特卡洛
在给一个矩阵形式吧,比较直观易懂
$$
V = R + \gamma PV
$$
4 马尔可夫决策过程(Markov decision preocess)
来到了强化学习经典五元组了
$$
<s, p, r, \gamma, a>
$$
a是action(动作)的意思,此外,接下来的状态转移都会加上动作,未来的状态不仅依赖于当前的状态,也依赖于在当前状态智能体采取的动作,奖励函数同理
$$
p(s_{t+1} \mid s_t, at) = p(s{t+1} \mid h_t, a_t) \
R(s_t = s, a_t = a) = \mathbb{E}[r_t \mid s_t=s, a_t=a]
$$
如何决定为动作,此时需要引入一个新变量
4.1 策略
策略定义了在某一个状态应该采取什么样的动作。知道当前状态后,我们可以把当前状态代入策略函数来得到一个概率,即
$$
\pi(a \mid s) = p(a_t=a \mid s_t=s)
$$
需要注意的是,策略是一个概率函数,这里可以分为两种,一种是取较大概率选择,另一种就是特地情况下随机选择,前者为后文的假设,后者可以理解为离子群,蚂蚁算法这样的意思
4.2 价值函数这一块
更新一下所有的价值函数,
$$
V{\pi}(s) = \mathbb{E}{\pi}[G_t \mid s_t=s]
$$
加入了策略
引入Q函数,定义为某一个状态采取某一个动作,有可能得到回报的期望
$$
Q{\pi}(s,a) = \mathbb{E}{\pi}[G_t \mid s_t=s,at=a]
$$
所以状态价值函数也同时可以定义为
$$
V{\pi}(s) = \sum{a \in A}\pi(a \mid s)Q{\pi}(s,a)
$$
贝尔曼方程也加入a,得
$$
Q(s,a) = R(s,a) + \gamma\sum_{s'\in S}p(s' \mid s,a)V(s')
$$
贝尔曼期望方程也是一个道理,就不放了
4 一些其他的定义
马尔可夫决策过程中的预测问题:即策略评估问题,给定一个马尔可夫决策过程以及一个策略$\pi$ ,计算它的策略函数,即每个状态的价值函数值是多少。其可以通过动态规划算法解决。
马尔可夫决策过程中的控制问题:即寻找一个最佳策略,其输入是马尔可夫决策过程,输出是最佳价值函数(optimal value function)以及最佳策略(optimal policy)。其可以通过动态规划算法解决。
最佳价值函数:搜索一种策略$\pi$ ,使每个状态的价值最大, $V^*$就是到达每一个状态的极大值。在极大值中,我们得到的策略是最佳策略。最佳策略使得每个状态的价值函数都取得最大值。所以当我们说某一个马尔可夫决策过程的环境可解时,其实就是我们可以得到一个最佳价值函数。
1.4.1 一些评价
预测和控制相辅相成,预测就是评价,当我选择策略$\pi$时,目前这条路的价值是多少,控制就是优化,需要找到最好的$\pi$。当这两个都最棒的时候(多目标优化),我们就找到了最佳价值函数