摘要(中)
物理信息神经网络(PINN)是一种神经网络(NNs),它编码模型方程,如偏微分方程(PDE),作为神经网络本身的一个组成部分。pinn目前被用于求解偏微分方程、分数方程、积分微分方程和随机偏微分方程。这种新颖的方法已经成为一种多任务学习框架,其中神经网络必须拟合观测数据,同时减少PDE残差。这篇文章提供了一个关于pinn的文献的全面回顾:而研究的主要目标是表征这些网络及其相关的优势和劣势。
这篇综述还试图结合更广泛的基于搭配的物理信息神经网络的出版物,这些出版物形成了基础PINN,以及许多其他变体,如物理约束神经网络(PCNN)、变分hp-VPINN和保守PINN (CPINN)。研究表明,大多数研究都集中在通过不同的激活函数、梯度优化技术、神经网络结构和损失函数结构来定制PINN。尽管pin已被广泛应用,但通过证明其在某些情况下比经典数值技术(如有限元法)更可行的能力,仍有可能取得进展,最明显的是仍未解决的理论问题。
摘要(英)
Physics-Informed Neural Networks (PINN) are neural networks (NNs) that encode model equations, like Partial Differential Equations (PDE), as a component of the neural network itself. PINNs are nowadays used to solve PDEs, fractional equations, integral-differential equations, and stochastic PDEs. This novel methodology has arisen as a multi-task learning framework in which a NN must fit observed data while reducing a PDE residual. This article provides a comprehensive review of the literature on PINNs: while the primary goal of the study was to characterize these networks and their related advantages and disadvantages. The review also attempts to incorporate publications on a broader range of collocation-based physics informed neural networks, which stars form the vanilla PINN, as well as many other variants, such as physics-constrained neural networks (PCNN), variational hp-VPINN, and conservative PINN (CPINN). The study indicates that most research has focused on customizing the PINN through different activation functions, gradient optimization techniques, neural network structures, and loss function structures. Despite the wide range of applications for which PINNs have been used, by demonstrating their ability to be more feasible in some contexts than classical numerical techniques like Finite Element Method (FEM), advancements are still possible, most notably theoretical issues that remain unresolved.
介绍
- PINN很适合求解微分方程(数学问题)
- PINN未来会很重要
- 目前的动力系统分类三概念 · 用那个神经网络 · 怎么表示物理知识 · 如何集成物理信息
PINN是什么?
一句话概括:将方程问题转化为损失函数优化问题,求PDE的解
举个例子
求解如下方程:
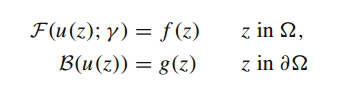
u为未知量,γ为与物理相关的参数,f为识别问题数据的函数,F为非线性微分算子,g表示边界函数。
u(z)由PINN计算预测,由一组参数θ参数化,从而产生近似
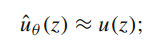
在通过一系列的变化之后,得到了以下方程,(每个数据有适当的加权)
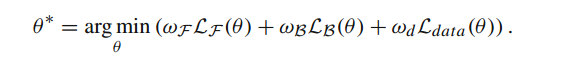
最后的神经网络图由下所示:(主要的目的还是为了求θ)
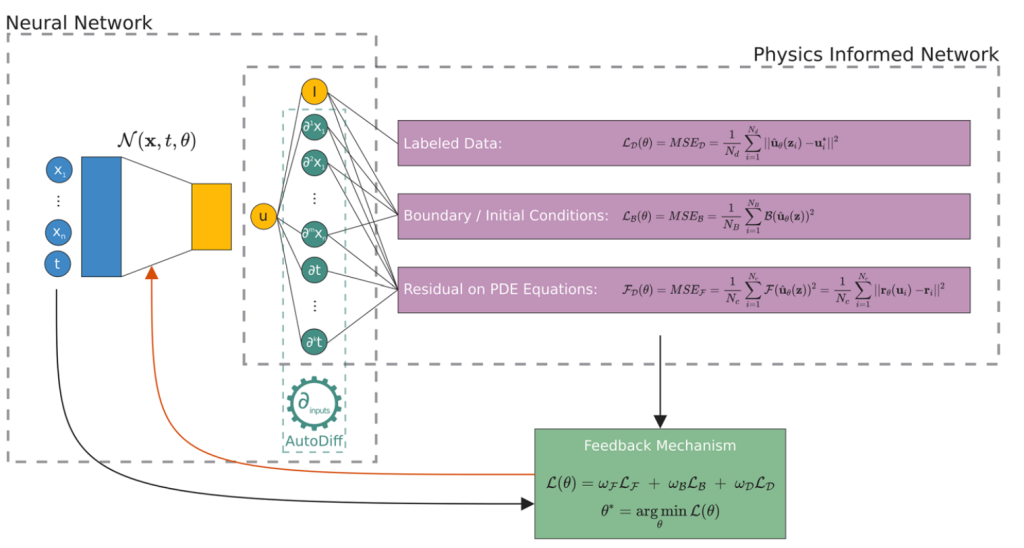
神经网络架构
基础神经网络
- FFNN(FNN),全连接前馈网络
- CNN(卷积神经网络)
- RNN(循环神经网络)
- DBN(深度信念网络)
- AE(自动编码器)
- GAN(生成对抗网络)
不熟悉的读者可以去了解一下,这篇文献只是介绍,我就不多写了
物理信息的与网络的融合
自动微分很重要(AD),一般用于对网络进行分析性评估。链式法则一般用于构建物理约束,即输入坐标并对神经网络进行微分
基于学习方法的模型评估
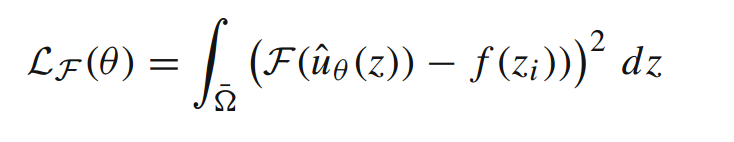
这个方程是由上面的公式推导出来的,很有用(我也不知道那里有用QAQ),可以以更高的频率采样,近似积分损失。
关于损失函数
主要用AD(自动微分)计算,惩罚项LF应有PDE约束
神经网络在求解时也可以在优化时去除方程的损失(W=0)
新概念:残差点,用于解决深层神经网络训练过程中的梯度消失和梯度爆炸问题
假设输入为x,网络的输出为H(x),残差连接可以表示为:H(x) = F(x) + x,其中F(x)表示网络的变换函数。通过引入残差连接,网络可以更容易地学习到残差F(x),而不需要过多地改变输入x的信息
在PINN中(仅限PINN哦😶🌫️),残差点的数量与损失函数的计算效率成负相关。因为我们需要更多的计算来处理残差点
硬约束与软约束
目前,许多现有的PINN框架使用一种软方法,通过在边界的并置点上创建额外的损失分量来约束bc
基于变分能量的损失函数更容易最小化(还没了解,欠着先),性能也更好。基于pde和基于能量的方法都有优点和缺点。基于pde的损失函数比基于能量的损失函数具有更多的超参数。与基于pde的策略相比,基于能量的策略对训练样本的大小和分辨率更敏感,但计算效率更高。
优化方法
如何让损失函数最小的过程就是优化过程,一般的优化方法为Adam和L-BFGS算法。
也有一种将两个算法相结合。先用带有预定义停止条件的Adam算法最小化损失函数,再通过L-BFGS-B优化器最小化损失函数
PINN理论
计算近似格式,以此计算真解u(z),如下公式:
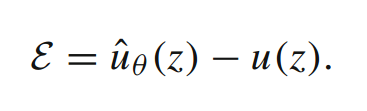
离散化的误差可以用一致性和稳定性来界定.当存在一致性和稳定性时,大致可以保证收敛性.
当使用PINN时,我们需要用物理定律建模的问题解决方案的参数化近似。一共有3个步骤:
- 收敛性方面,证明其为收敛=有解
- 统计学习误差分析,最重要的是需要考虑优化,泛化误差与近似误差
- 误差分析结果
PINN求解微分方程
常微分方程(Ordinary Differential Equations)
该方程一般用于模拟复杂的非线性系统。最经典的样子就是
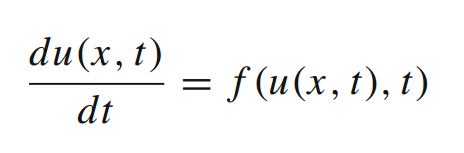
初始条件可指定为B(u(t)) = g(t),从而得到B(u(x)) = g(x)的初值问题或边值问题。接着,利用神经网络i以ODE的形式进行参数化
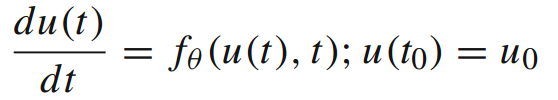
在此,将ODE结构分为两部分:物理信息项与未知差异项
偏微分方程(Partial Differential Equations)
- 稳态PDE
- 非稳态PDE
分数阶方程
分数阶偏微分方程可用于模拟自然界中发现的各种各样的现象学特性,这些特性的参数必须从实验数据中计算出来。由于自动微分不适用于分数阶算子,因此分数阶模型的pin n的构建更为复杂。可以使用L1范数进行计算
实例(tm终于看到实际例子了😭😭😭)
给定一个方程组与域δ = [- 5,5] × (0, T),其中,T为π/2
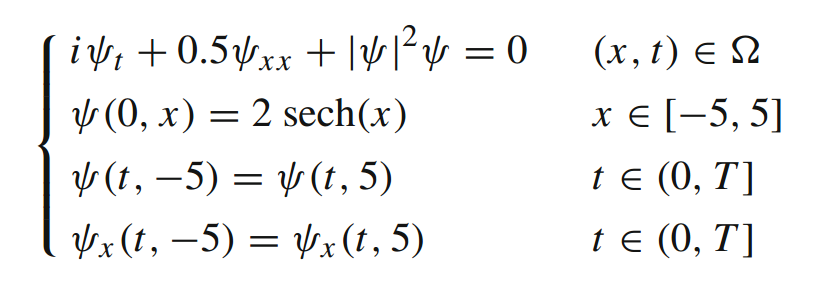
该神经网络输入两个值,分别为时间t与位置x。训练的目的为使边界条件LB造成的损失最小化,并且满足该方程。该损失函数为
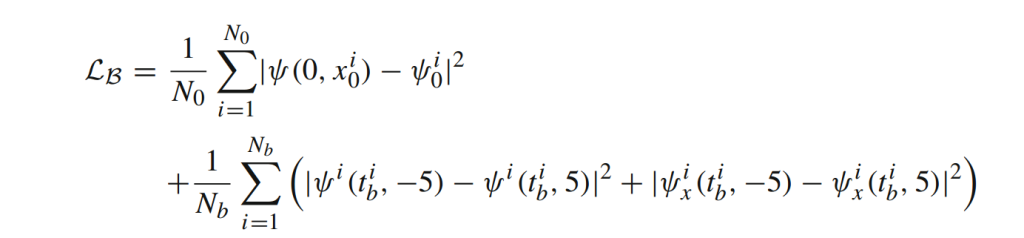
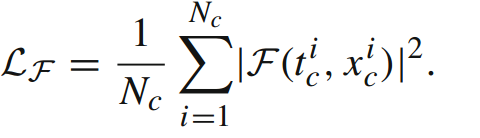
在有了损失函数后,我们使用Adam,学习率为10^-3。再使用LBFGS进行微调(143)
PINN的应用
- 血液动力学
- 流问题
- 光学与电磁应用
- 分子动力学和材料相关应用
- 地球科学和弹性静力学问题
- 工业应用
PINN相关软件与包调用
- NeuroDiffEq(基于pytorch)
- DeepXDE(库)
- Modulus(N卡)
- SciANN(基于Keras)
- TensorDiffEq